
26 Août La constellation des mégalithes de Bezonnes : un puzzle géométrique
Longtemps, les mégalithes ont été abordés comme des éléments isolés et autonomes, sans relation les uns avec les autres.
C’est souvent sur les cromlechs – cercles de pierres, que le rapport des stèles entre elles a fait émerger des alignements ou des figures géométriques singulières.
Sur le plateau large d’environ 10 kilomètres qui relie Bezonnes à Salles-la Sources en Aveyron, ce sont plus de 100 mégalithes qui ont été recensés.
De loin, Menhirs et Dolmens semblent réparties de manières uniformes sur le territoire. En y regardant de plus près, ils forment parfois des groupes sous forme de grappe.
La question demeure : ces mégalithes relativement rapprochés ont-ils été placés les uns par rapport aux autres, et si oui avec quelle relation ? Autrement dit, ces mégalithes peuvent-ils tisser un réseau, un maillage cohérent sur le territoire ?
Dans un précédent article, <https://argemaformation.com/le-carre-de-bezonnes-deux-megalithes-en-aveyron/> nous avons montré la relation entre deux dolmens en particulier.
En restant sur ce même théâtre, nous faisons intervenir d’autres acteurs qui joueront et viendront compléter un puzzle rhizomatique.
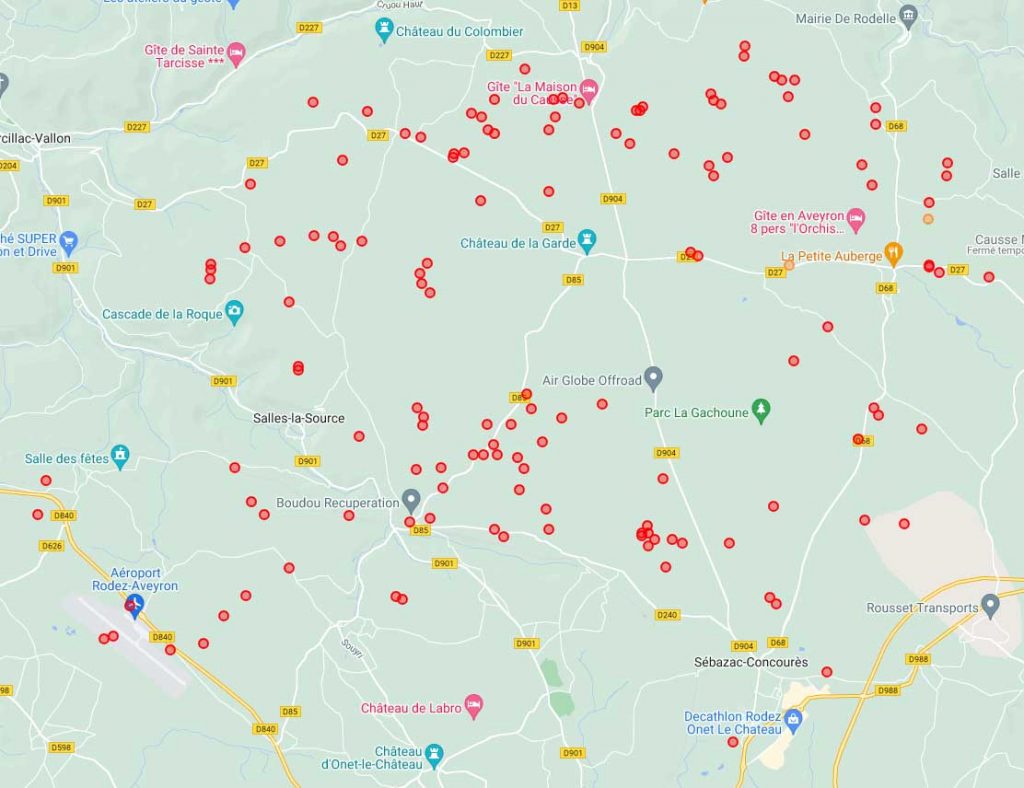
Trouver le bout la pelote de laine : par où commencer ?
Si l’on considère l’ensemble des relations possibles des 100 mégalithes entre eux, le nombre de combinaisons devient vite gigantesque.
Imaginons qu’il faille regarder pour chaque dolmen quelle est sa position relative vis-à-vis des 99 autres : cela fait beaucoup de possibilités.
Nous avons réalisé pour cet article un dessin où chaque dolmen est relié par un trait aux 99 autres mégalithes : le résultat est pour le coup vraiment parlant. C’est un dessin peut être joli, mais qui montre la densité du maillage, et l’impossible lecture d’un tel graphique tant la densité des traits est grande et sature l’espace.
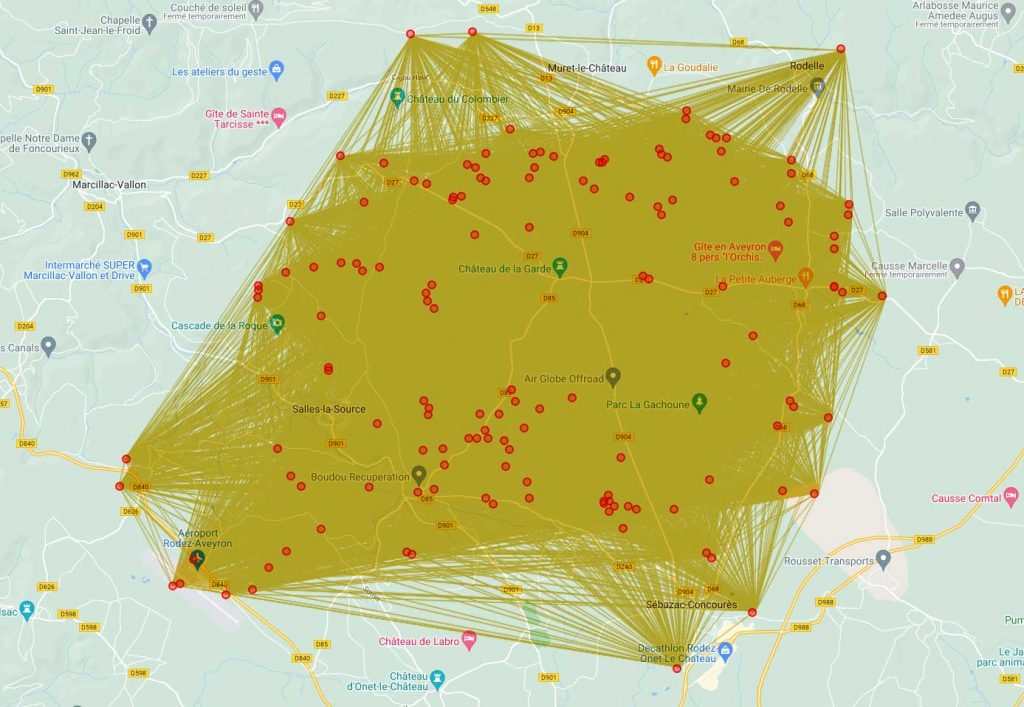
Cette démarche de tout vouloir absolument relier ouvre la porte à trop de possibles, sans aucun fondement légitime, dans lesquels il est possible de se perdre.
C’est donc une autre approche qu’il faut suivre, en se resserrant sur moins d’objets.
Le complexe de Bezonnes
Voici 6 points autour du village de Bezonnes qui correspondent à 6 mégalithes. À l’ouest le dolmen de Dalmerac (ou sahnes), les deux menhirs de Bezonnes au centre, et les Dolmens de Bezonnes 1, 2 (ou roc de la Françouna) et 3.
Les points sur la carte sont cliquables
Parmi ces 6 points nous connaissons déjà le lien de deux d’entre eux où nous avions émis une hypothèse où les dolmen 1 et 2 se reliaient en formant la diagonale d’un carré parfaitement aligné sur les axes nord/sud et est/ouest.
Mais voyons ce qui se passe en élargissant la zone pour faire rentrer en jeu ces 4 autres mégalithes.
D’un premier abord, la cohérence entre ces points ne saute pas aux yeux. Nous allons essayer de tester plusieurs façons de les relier.
Le graph : un peu de mathématique.
S’attaquer à l’interaction de plusieurs points entre eux s’étudie en mathématique avec la notion de Graph. Ces outils mathématiques sont appliqués dans différents domaines : comprendre la relation entre des personnes, entre des villes, entre des ordinateurs… un peu tout ce qui fait appel au réseau : réseau d’amitié, réseau aérien, réseau informatique.
La définition du graph est relativement simple : il est composé de sommet (points) et des arêtes reliant ces points.
La première hypothèse serait de créer un chemin qui passe par tous les points en formant un polygone, pas vraiment régulier.
Dans ce cas-là, nous avons bien la relation entre nos deux dolmens déjà étudiés.
Mais essayons autre chose.
Dans ce deuxième dessin, nous regardons toutes les combinaisons : chaque point est relié aux autres.
Mais est-on certain que ces relations existent bel et bien ?
Mesurer pour faire du tri
La première méthode consiste à étudier les longueurs remarquables entre les mégalithes.
Sans noter toutes les longueurs de toutes les combinaisons, voici déjà certaines distances qui nous intéressent. Remarque : comme déjà observé, nous allons non pas utiliser l’unité métrique, mais le yard mégalithique (environ 0,83 m) qui a déjà observé sur le site du causse ou un l’un de son multiple la Toise mégalithique (2,07 m).
| DOLMEN DE DALMAYRAC 1 | DOLMEN ROC DE LO FRONÇOUNA | DOLMEN DE BEZONNES 1 | DOLMEN DE BEZONNES 3 | MENHIR BEZONNE 01 | MENHIR BEZONNE 02 | |
|---|---|---|---|---|---|---|
| DOLMEN DE DALMAYRAC 1 | x | 2 497YM ou 998 TM | ||||
| DOLMEN ROC DE LO FRONÇOUNA | x | x | 1500 YM ou 600 TM | |||
| DOLMEN DE BEZONNES 1 | x | x | x | |||
| DOLMEN DE BEZONNES 3 | x | x | x | x | 204,09 YM | |
| MENHIR BEZONNE 01 | x | x | x | x | x | |
| MENHIR BEZONNE 02 | x | x | x | x | x | x |
Ce premier travail de mesure finalement pas trop fastidieux pour ces 6 points montre déjà quelques relations intéressantes pour 3 couples, lorsque les mesures approchent des nombres « ronds » comme 200, 1 500, 2 500…
Et que dit le rapporteur d’angle?
Après avoir regardé les distances, nous pouvons superposer une deuxième grille de lecture qui s’intéresse aux angles mesurés entre ces points.
| DOLMEN DE DALMAYRAC 1 | DOLMEN ROC DE LO FRONÇOUNA | DOLMEN DE BEZONNES 1 | DOLMEN DE BEZONNES 3 | MENHIR BEZONNE 01 | MENHIR BEZONNE 02 | |
|---|---|---|---|---|---|---|
| DOLMEN DE DALMAYRAC 1 | x | 71,60°N (diagonale d'un triple carré) | 90°N = axe Est/ouest | |||
| DOLMEN ROC DE LO FRONÇOUNA | x | 135°N (diagonale d'une carré) | 179°N axe Nord/sud | |||
| DOLMEN DE BEZONNES 1 | x | x | x | |||
| DOLMEN DE BEZONNES 3 | x | x | x | x | 118°N ( approche d'un recangle racine de 3) | |
| MENHIR BEZONNE 01 | x | x | x | x | x | |
| MENHIR BEZONNE 02 | x | x | x | x | x | x |
Ici, les angles remarquables sont au nombre de 5, avec des superpositions entre des relations déjà relevés par les mesures. Ces angles, correspondent soit aux côtés ou aux diagonales de rectangles dits remarquables positionnés sur les axes cardinaux. Les carrés, doubles et triples, ou rectangle « racine » en font partie.
Voici les figues géométriques que nous relevons.
La constellation
À l’aide de cette méthode qui recoupe mesure des distantes et mesure des angles, nous pouvons établir d’hypothétiques relations des pierres entre elles.
Comme pour relier les étoiles entre elles nous arrivons à une sorte de « constellation » de mégalithes.
On peut remarquer que certains mégalithes comme le dolmen de Bezonnes 3 n’ont de relation qu’avec un seul autre mégalithe.
En revanche, d’autres comme le Roc de la Françouna, interagit géométriquement avec 3 autres. On peut noter aussi que ce dernier est aussi le plus imposant de tous, et qu’il aura sûrement joué un rôle « pivot » important dans l’implantation des pierres.
Pour autant, il n’y a pas forcément d’ordre ou de hiérarchie réellement définie qui pourrait penser à une chronologie dans l’élaboration du plan.
C’est plutôt une structure en rhizome qui se dégage où chaque mégalithe est le relais de l’autre.
À noter aussi : le dolmen de Bezonne 1 et 3 qui sur la carte qui semblaient proches n’ont finalement pas d’interaction géométrique.
Relations avec des mégalithes de différentes natures.
L’idée pourrait être a priori de n’envisager les relations qu’avec des mégalithes de même type : les menhirs avec les menhirs les dolmens qu’avec les dolmens.
Or, comme nous l’avons relevé, une relation géométrique entre un dolmen et un menhir peut exister.
Pour le tissage du réseau mégalithique, ce n’est pas forcément la forme de la construction en pierre qui prône, mais plutôt son positionnement.
La décentralisation avant l’heure
Pourquoi s’intéresser au Concept de graphe ?
Il est intéressant de considérer les avantages d’une structure sans réel centre, mais qui utilise une structure de type rhizome.
C’est le cas par exemple pour une station d’une ligne de métro à Paris : si une station est fermée pour travaux, le maillage est assez dense pour pouvoir s’en passer, la contourner et arriver à sa destination. Idem pour le réseau internet où l’information est répartie dans plusieurs serveurs à la fois.
Il en va de même pour des mégalithes : le temps a fait disparaître un certain nombre par érosion, destruction, déplacement… pour autant, les structures reliant les mégalithes entre eux, même partielle, peuvent rester toujours présentes.
On voit là une grande force d’une telle implantation, qui assure à ce type de sanctuaire une longévité de plus de 4 000 ans.
La relation géométrique des mégalithes entre eux a déjà été démontrée sur d’autres territoires comme en Bretagne par le chercheur Howard Crowhurst.
Cette géométrie à grande échelle semble être le ciment du maillage mégalithique. Les exemples sont très nombreux et bien présents en Aveyron et dans la partie sud de la France en général.
Durer dans le temps, avoir une activité pérenne… un objectif pour la géobiologie.
Dans ses interventions, le géobiologue a tout intérêt de poser des dispositifs qui “tiendront” dans le temps.
Le géobiologue peut s’inspirer du modèle des anciens pour venir structurer un lieu.
Nul besoin d’avoir à ajuster car “ça aurait bougé”.
En effet, c’est au géobiologue d’envisager son intervention de façon pérenne par exemple lors de la pose d’une pierre, de l’implantation d’une maison ou autre intervention.
Comprendre pour mieux ressentir
Lorsque l’on rend visite à un mégalithe, le plaisir de la rencontre est aussi d’essayer de ressentir le lieu.
Au travers de sa propre biosensibilité, il est possible, comme dans une chapelle, ou une cathédrale, de s’ouvrir et de relationnel avec la pierre.
Cette approche qui n’appartient plus au monde rationnel n’est pas sans intérêt, bien au contraire.
Toutefois, connaître à travers une étude géométrique, plus “terre à terre”, les relations des pierres entre elles, enrichi le champ du ressenti.
Grâce à ce savoir, on ne se contentera pas d’apprécier le lieu seul, mais de prendre conscience d’un espace beaucoup plus vaste.
Pour ainsi dire, cette géométrie ouvre les esprits.
L’étude des mégalithes est vraiment un terrain de jeux formidable pour le géobiologue qui cherche à s’aguerrir.
Mieux connaître ces pierres constitue un bagage solide qui permettra de comprendre des constructions bien plus contemporaines.
Nous reviendrons dans un prochain article avec les mêmes outils sur le fonctionnement d’une mystérieuse architecture beaucoup plus récente située au centre même de la France : la Pyramide de Saint-Amand Montrond.
Benoît Blein
Pour citer cet article : Benoît Blein, Le carré de Bezonnes : deux mégalithes en Aveyron, https://argemaformation.com/la-constellation-des-megalithes-de-bezonnes-un-puzzle-geometrique/ le 26 aout 2022.
Illustrations : ©Benoît Blein 2022
Argema Formation – École Nationale de Géobiologie Appliquée.
Demande d’information complémentaire.
Benoît Blein est géobiologue et graphiste en Aveyron
Il anime à Argema Formation un nouveau module Compréhension du monde Mégalithique

Pour joindre l’auteur :
benoit@fusainblanc.com
Tél. : 06 86 84 92 06
Saint-Ferréol, le 26 aout 2022.
DU MÊME AUTEUR, D’AUTRES ARTICLES DÉJÀ PARUS SUR LE SUJET À DÉCOUVRIR OU RELIRE :
Approche du monde Mégalithique : un modèle d’inspiration pour la géobiologie






